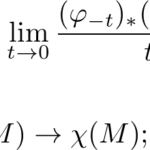接続という概念に最初に出会うのはリーマン幾何学のLevi-Civita接続だと思います。Levi-Civita接続は計量を保つ捩れのない接続と定義されますが、接続の「捩れ」は幾何学的な理解がかなり難しい概念のように思います。そこで捩れの理解のために接続にまつわる話題をまとめてみようと思ましたが、長くなりそうなので「接続の幾何」というタイトルでシリーズ化することにしました。この記事は接続の幾何シリーズの1つ目の記事です。
- 「ファイバー束の接続(接続の幾何1)」← 今ここ
- 「主束の接続と曲率 : 最短解説(接続の幾何2)」
- 「接続の捩れと接枠バンドル(接続の幾何3)」
- 「リーマン幾何学の捩れテンソルの意味 : 最短性と真っ直ぐさ(接続の幾何:番外編1)」
接続はリーマン幾何学以外にも、バンドルの特性類を曲率を用いて表す Chern-Weil 理論や、接続全体の集合から微分構造の情報を得るゲージ理論など、色々な場面で現れます。捩れは接ベクトル束についての概念ですが、より一般的な枠組みから接続について理解することは損にはならないし、その方がわかりやすいのではと思い、ファイバー束の接続から入ることにしました。
本記事での定義は [森田1] を参考にしています。以下の記事では接ベクトル束上の接続を、接ベクトルの方向微分を与えるものと述べましたが、それとの関係についても述べたいと思います。
目次
ファイバー束
ファイバー束の定義
まずはファイバー束の定義をします。概ね、ベクトル束のファイバーをベクトル空間から多様体に置き換えたものと思っていいです。
定義. ファイバー束
$F$ を $C^{\infty}$ 多様体とする. $C^{\infty}$ 多様体 $E, B$ と $C^{\infty}$ 写像 $\pi : E \to B$ が与えられ, 次の条件を満たすとき, $\xi = (E, \pi, B, F)$ を $F$ をファイバーとするファイバー束という.
(条件) $B$ 上の任意の点 $b$ に対し, $B$ の開近傍 $U$ と微分同相 $\varphi: \pi^{-1}(U) \to U \times F$ が存在して, 任意の $u \in \pi^{-1}(U)$ に対し、$\pi(u) = \pi_1 \circ \varphi(u)$ となる. ここで, $\pi_1$ は第一成分への射影である.$\Box$
上記の条件に出てきた $\varphi$ を局所自明化といいます。また、$E$ を全空間、$B$ を底空間、$F$ をファイバー、 $\pi$ を射影といいます。さらに、混同の恐れがないときは $(E, \pi, B, F)$ の代わりに $\pi: E \to B$ または $E$ をファイバー束と呼びます。
構造群とは
$\{U_{\alpha}\}$ を底空間 $B$ の開被覆とすると、定義から各開集合 $U_{\alpha}$ 上の自明化
$$\varphi_{\alpha} : \pi^{-1} (U_{\alpha}) \cong U_{\alpha} \times F$$
が存在します。$U_{\alpha} \cap U_{\beta}$ 上での同型
$$\varphi_{\alpha} \circ \varphi_{\beta}^{-1} : (U_{\alpha} \cap U_{\beta}) \times F \cong (U_{\alpha} \cap U_{\beta}) \times F$$
を考えると、これは各点ごとのファイバーの同型を与えています。$F$ の微分同相写像の集合を $\mathrm{Diff}\ F$ とおくと、写像
$$g_{{\alpha}{\beta}} : U_{\alpha} \cap U_{\beta} \to \mathrm{Diff}\ F$$
が存在して、
$$\varphi_{\alpha} \circ \varphi_{\beta}^{-1} (b, p) = (b, g_{\alpha\beta} (b) (p)) \ \ (b \in U_{\alpha} \cap U_{\beta}, p \in F)$$
と表されます。$g_{\alpha\beta}$ をファイバー束 $\xi$ の変換関数といいます。変換関数の族 $\{g_{\alpha\beta}\}$ はコサイクル条件
$$g_{\alpha\beta}(b) g_{\beta\gamma}(b) = g_{\alpha\gamma}(b) \ \ (b \in U_{\alpha} \cap U_{\beta} \cap U_{\gamma})$$
を満たします。逆に、$B$ の開被覆 $\{U_{\alpha}\}$ と関数の族 $\{g_{\alpha\beta}\}$ が与えられると、ファイバー束がファイバー束が構成出来ます。この辺りはベクトル束の場合と同じです。ただし、ベクトル束のと異なるのは、変換関数の値域が $\mathrm{Diff}\ F$ と非常に大きな群である点です。実際、ファイバーが $\mathbb{R}^n$ のファイバー束を定義通りにみると、変換関数の値域は $\mathrm{Diff}\ \mathbb{R}^n$ となります。しかし、ベクトル束の定義では、変換関数は $GL_n \subset \mathrm{Diff} \ \mathbb{R}^n$ でした。
ファイバー束でも、変換関数の値域がもっと小さい群の場合を考えることがあります。底空間の開被覆 $\{U_{\alpha}\}$ と 変換関数の族 $\{g_{\alpha\beta}\}$ を、$\{g_{\alpha\beta}\}$ の値域が部分群 $G \subset \mathrm{Diff} \ F$ に含まれるようにとれるとき、$(E, \pi, B, F , G)$ を $G$ を構造群とするファイバー束といい、$G$ を構造群といいます。
主束とは
$G$ を構造群とするファイバー束は、開被覆 $\{U_{\alpha}\}$ と変換関数 $\{g_{\alpha\beta}\}: U_{\alpha} \cap U_{\beta} \to G$ によって構成できます。そして、この構成方法には $F$ についての条件はありません。よって、$F$ を $G$ が作用する別のファイバー $F^{\prime}$ に置き換えて別のファイバー束を構成することが出来ます。例えば、ファイバーが $S^1$ で、構造群が回転群 $SO(2)$ のファイバー束を考えます。$SO(2)$ は $\mathbb{R}^2$ に自然に作用するので、ファイバーを $\mathbb{R}^2$ に置き換えると、$\mathbb{R}^2$ をファイバーとするファイバー束が構成されます。このように、同じ変換関数を持つとき、ファイバー束は互いに同伴するといいます。
ファイバーが $G$、構造群が $G$ のファイバー束で、構造群 $G$ のファイバー $G$ への作用が自然な左作用であるとき、$(P, \pi, B, G, G)$ を $G$ を構造群とする主束 (principal bundle)または主 $G$ 束といいます。主束であることを強調するため、全空間を $E$ ではなく $P$ とします。ファイバー束の定義から、$G$ は$C^{\infty}$ 多様体で自身への作用は微分同相なので、$G$ はLie群になります。
主 $G$ 束 $P$ には $G$ の右作用が、各ファイバーに $G$ を右から作用させることで定義されます。この作用が自明化の取り方によらないことは、任意の変換関数 $g_{\alpha\beta}$ と $(b, h) \in (U_{\alpha} \cap U_{\beta}) \times G$ に対し、
$$ g_{\alpha\beta}(b) (hg) = (g_{\alpha\beta}(b)h) g$$
が成り立つことからわかります。左辺は $g$ を作用させてから変換したもの、右辺は変換してから $g$ を作用させたものでありそれらが等しいです。( $G$ 自体には左からの作用が考えられますが、変換関数と可換ではないので $P$ への左作用は一般には定義できません。)
逆に、$P$ を滑らかな多様体、$G$ をLie群とし、$G$ の $P$ への右作用が適当な条件を満たすとき、$P$ は $\pi: P \to P / G$ を射影とする主束の構造を持つようです。ここでは、$P$ を構造群を $\mathrm{Diff} \ G$ とするファイバー束とし、$G$ が $P$ にファイバーごとに右から作用するときに、$P$ が主束であることを確認します。
$u \in P$ とし、 $b = \pi(u) \in U_{\alpha} \cap U_{\beta}$ であるとします。$\varphi_{\alpha}(u) = (b, h_{\alpha})$, $\varphi_{\beta} (u) = (b, h_{\beta})$ とおきます。このとき、
$$g_{\alpha\beta}(b)(h_{\alpha}) = h_{\beta}$$
を満たします。$g \in G$ が右から作用するので、
$$g_{\alpha\beta}(b)(h_{\alpha} g) = h_{\beta} g$$
を満たします。よって $g$ の代わりに $h_{\alpha}^{-1} g$ を右から作用させれば、任意の $g \in G$ に対して
$$g_{\alpha\beta}(b)(g) = h_{\beta} h_{\alpha}^{-1} g$$
が成り立ちます。したがって、$g_{\alpha\beta} (b) = h_{\beta} h_{\alpha}^{-1} \in G$ であり、構造群は $G$ に縮小します。よって、$P$ は 主 $G$ 束になります。
ファイバー束の接続
接続の定義
(主束とは限らない)ファイバー束 $\pi: E \to B$ の接ベクトル束 $\tau^E: TE \to E$ を考えましょう。$\pi$ の微分 $\pi_*: TE \to TB$ と $\tau^{B}: TB \to B$ について、以下の図式は可換になります。
\begin{xy} \xymatrix{ TE \ar[r]^{\tau^E} \ar[d]_{\pi_*} & E \ar[d]^{\pi} \\ TB \ar[r]^{\tau^B} & B } \end{xy}
$u \in E$, $b = \pi(u)$ とすると、$\pi_* |_{T_u E}: T_u E \to T_b B$ はファイバー方向のベクトルを潰す射影になります。$V_u = \operatorname{Ker} (\pi_* |_{T_u E}) \subset T_u E$ とおき、$V_u$ に属するベクトルを垂直方向ベクトルと呼びます。
垂直方向は上記のように定めることができましたが、水平方向はどのように定められるでしょうか。ここで、水平方向が定まるとは、$V_u \oplus H_u = T_u E$ を満たす部分空間 $H_u$ が与えられることとします。
ファイバー束が直積 $B \times F$ である場合は、射影 $\pi_2 : B \times F \to F$ の微分 ${\pi_2}_*: T (B \times F) \to TF$ の核を水平方向とすることが出来ます。よって、自明化 $\varphi_{\alpha}: \pi^{-1}(U_{\alpha}) \to U_{\alpha} \times F$ が与えられれば $U_{\alpha}$ 上で水平方向が定まります。しかし、これは自明化の取り方に依存してしまいます。実際、変換関数 $g_{\alpha\beta}$ は底空間 $B$ の値に依存するので、微分 ${g_{\alpha\beta}}_* : TB \to T (\mathrm{Diff} \ F)$ が $0$ でなく、その分のずれが生じます ( $T (\mathrm{Diff} \ F)$ が定義できるか不明ですが、とりあえず $F$ 上のベクトル場全体の集合と思ってください)。
実はファイバー束の定義だけでは水平方向を一意に定めることが出来ません。そこで各点 $u \in E$ 上で $H_u \oplus V_u = T_u E$ を満たす部分空間 $H_u \subset T_u E$ を強引に与え、それを接続と呼ぶこととします。主束 $(P, \pi, B, G)$ の場合はさらに、 $g \in G$ の右作用で不変であることを仮定します。つまり、$g$ の右作用を $R_g: P \to P$ としたとき、$({R_g}_*) (H_u) = H_{ug}$ を満たすとします。
水平持ち上げ
水平方向が定まると、$\pi_* |_{H_u}: H_u \simeq T_{\pi(u)}B$ により $B$ の接ベクトルを $E$ の接ベクトルに持ち上げることができます。これが開集合 $U_{\alpha}$ 上の局所自明化によってどう表されるか確認しましょう。$(b, p) \in U_{\alpha} \times F$ とし、$T_b B$ の基底を $\{e_1, \dots, e_n\}$、$T_p F$ の基底を $\{v_1, \dots, v_m\}$ とします。$T_{(b, p)}$ は
$$T_{(b, p)} = T_bB \oplus T_pF = H_{(b, p)} \oplus V_{(b, p)}$$
の二つの直和分解を持ちます。$V_{(b, p)} = T_pF$ であり、その基底は $\{v_1, \dots, v_n\}$ です。$e_i$ の $T_bB \oplus T_pF$ での垂直方向への射影は $0$ ですが、$H_{(b, p)} \oplus V_{(b,p)}$ での垂直方向の射影は $0$ とは限らないことに注意しましょう。
$(\pi_*|_{H_{(b, p)}})^{-1}$ と射影 $T_bB \oplus T_pF \to T_pF$ の合成を $A: T_b B \to T_p F$ としたとき、 $H_{(b, p)}$ の基底は $\{e_1 + Ae_1, \dots, e_n + Ae_n\}$ と表されます。逆に $A: T_b B \to T_p F$ が定まれば、$\{e_1 + Ae_1, \dots, e_n + Ae_n\}$ を基底とする部分空間 $H_{(b, p)}$ が一意的に定まります。よって局所自明化の上では、接続を与えることと各点で線型写像 $A: T_b B \to T_p F$ を与えることが同値になります。これによって、各点での線型写像の足し算、スカラー倍をとることによって、接続に足し算やスカラー倍を定義することが出来ます。
接ベクトル束の接続との比較
記事「多様体上のリー微分と接続の共通点と相違点」では、ベクトル束の接続を平行移動の観点で説明していました。ここでも、平行移動の観点で接続を見てみましょう。まずは、ファイバー束の平行移動を定義してみましょう。
ファイバー $F$ がコンパクトであるか $E$ が主束の場合には、$B$ 上の滑らかな曲線 $c: [t_0, t_1] \to B$ の各点で $\frac{dc}{dt}$ を持ち上げ、$P$ 上で積分曲線を取ることで、$P$ 上の曲線 $\tilde {c}$ に持ち上げられます (コンパクト性などの条件の必要性については [森田1] をご参照ください)。これにより、ベクトル束の場合と同様に曲線 $c$ に沿った平行移動を定められます。$\tilde{c}$ の始点は $\pi^{-1}(t_0)$ の任意の点を取れ、各 $t_0 \leq t \leq t_1$ に対し $\pi(\tilde{c}(t)) = c(t)$ を満たし、さらに微分方程式の解の一意性から積分曲線は交わらないため、微分同相
$$\Pi (c)_{t_0}^{t}: \pi^{-1}(c(t_0)) \to \pi^{-1}(c(t)) $$
が定まります。これを平行移動といいます。一般の場合ファイバーに引き算が定められないので、平行移動から共変微分は定義できません。
ベクトル束の場合、平行移動は線型写像でしたが、上記では微分同相になっています。この違いはどこから来ているのでしょうか。実はベクトル束の接続はファイバー束の接続より強い条件を課しています。
$F \simeq \mathbb{R}^n$ とします。ファイバー束の接続では $u, u^{\prime} \in \pi^{-1}(b)$ の水平方向 $H_u, H_{u^{\prime}}$ は独立に定められました。しかし、ベクトル束の接続は水平方向に、ファイバーの元に対応する線形性を課します。つまり、
$$H_{au + a^{\prime}u^{\prime}} = aH_u + a^{\prime} H_{u^{\prime}}$$
を満たすとします。ただし、水平方向の足し算とスカラー倍は $F \simeq \mathbb{R}^n$ より定まる自然な同一視 $T_u F \simeq T_{u^{\prime}} F \simeq \mathbb{R}^n$ と前述した線型写像 $A: T_b B \to T_u F$ の足し算、スカラー倍で定めるものとします。
この条件から平行移動が線型写像になることを示しましょう。曲線 $c$ に沿ったベクトル場を接続により持ち上げることで、$\pi^{-1} (c)$ 上のベクトル場 $X$ が得られます。$u, u^{\prime} \in \pi^{-1}(c(t))$ とすると、接続の定義から
$$X_{au + a^{\prime} u^{\prime}} = aX_u + a^{\prime} X_{u^{\prime}}$$
を満たします。$u_0, u_0^{\prime} \in \pi^{-1}(c(t_0))$ を始点とする $c$ の持ち上げをそれぞれ $\tilde{c}, \tilde{c}^{\prime}$ としたとき、$a \tilde{c} + a^{\prime}\tilde{c}^{\prime}$ は $\pi^{-1}(c)$ 上の曲線になりますが、微分をするとベクトル場 $X$ の $a u_0 + a^{\prime} u_0^{\prime}$ を始点とする積分曲線上のベクトル場と一致することがわかります。よって始点で足し算、スカラー倍してから平行移動するのと、平行移動してから足し算、スカラー倍するのが同じになります。よって、平行移動は線型写像になります。平行移動が線型写像であることが確認できたため、これによってベクトル束上の共変微分を定義できます。
ファイバー束の接続を、全空間の接空間の水平方向を定めることで定義しましたが、以上によって接ベクトル束の接続と等価であることがわかりました。
最後に、ベクトル束の接続は局所的にはクリストッフェル記号で表されますが、これについて簡単に触れましょう。水平方向 $H_u$ は線型写像 $A_u: T_b B \to T_p F$ によって定まるのでした。$A_u$ はファイバーの元について線型なので、$\pi^{-1}(b)$ の基底に対して $A_u$ を定めれば $\pi^{-1}(b)$ 上の各点の水平方向が定まります。よって、底空間のベクトルとファイバーの点 $F \simeq \mathbb{R}^n$ が与えられると $T_p F \simeq F \simeq \mathbb{R}^n$ の元が与えられます。それぞれの基底を与えるとそれに応じて値が定まり、それがクリストッフェル記号と一致します (符号は異なるかもしれません)。
まとめ
ファイバー束の接続を、ファイバー束上の各点の接空間の水平方向を与えることで定義し、それがベクトル束上の共変微分として与えられる接続の自然な一般化であることを確認しました。
次回は主束の場合の接続をより詳しく調べ、その曲率について述べたいと思います。
- 次の記事「主束の接続と曲率 : 最短解説(接続の幾何2)」
参考文献
[森田1] 森田茂之. 微分形式の幾何学
ご支援のお願い
記事を読んで、「支援してもいいよ」と思っていただけましたら、ご支援いただけると幸いです。サーバー維持費などに充てさせていただきます。登録不要で、100円から寄付でき、金額の90%がクリエイターに届きます。