可微分多様体 $M$ には接ベクトル束 $\pi : TM \to M$ が自然に定義される。接ベクトル空間は多様体の次元と同じ次元のベクトル空間なので、異なる2点 $p, q \in M$ の接ベクトル空間 $T_pM, T_qM$ は同型である。しかし、これらの間の自然な同型は存在しない。その為、別の点での接ベクトル $v_p \in T_pM, v_q \in T_qM$ を比較するには、それらの間の同型を何らかの方法で定める必要がある。リー微分や接続では、意味合い的には別の点での接ベクトルの差を比較している。その辺りの整合性の取り方を焦点に、これらを解説しようと思う。
その前に、ベクトル場 $X$ の、点 $p \in M$ での $v_p \in T_pM$ への方向微分 $v_p(X)$ は座標変換で保たれないことに注意する。例えば、$f(x_1, x_2) = (x_1x_2, x_2)$ を $\mathbb{R}^2$ の $(1, 1)$ の近傍から $(1, 1)$ の近傍への微分同相とし、$v = \frac{\partial}{\partial x_1}, X = \frac{\partial}{\partial x_2}$ とする。普通に計算すると $v(X) = 0$ である。一方、$y_1 = x_1x_2, y_2 = x_2$ と置いたとき、
$$\frac{\partial}{\partial x_1} = \frac{\partial y_1}{\partial x_1}\frac{\partial }{\partial y_1} + \frac{\partial y_2}{\partial x_1}\frac{\partial }{\partial y_2} = y_2\frac{\partial }{\partial y_1}$$ $$\frac{\partial}{\partial x_2} = \frac{\partial y_1}{\partial x_2}\frac{\partial }{\partial y_1} + \frac{\partial y_2}{\partial x_2}\frac{\partial }{\partial y_2} = \frac{y_1}{y_2}\frac{\partial }{\partial y_1} + \frac{\partial }{\partial y_2}$$
であるから、$v(X) = \frac{\partial }{\partial y_1} \neq 0$ となり、座標変換で値が保たれない。
リー微分について
さて、まずはリー微分について解説する。リー微分ではベクトル場のフローを用いることで異なる接空間のベクトルを比較する。
$X$ を $M$ 上のベクトル場とし、 $X$ を積分して得られるフローを $\varphi_t : M \to M, (t \in \mathbb{R})$ とする。$\varphi_t$ は任意の $t$ で微分同相なので、$\varphi_t(p) = q$ となる $p, q \in M$ に対して、$\varphi_t$ の微分 $(\varphi_t)_* : T_pM \to T_qM$ は接ベクトル空間の間の同型を定める。これによって、異なる点の間の接ベクトルを比較できるようになる(ただしフローで移り合う点に限る)。
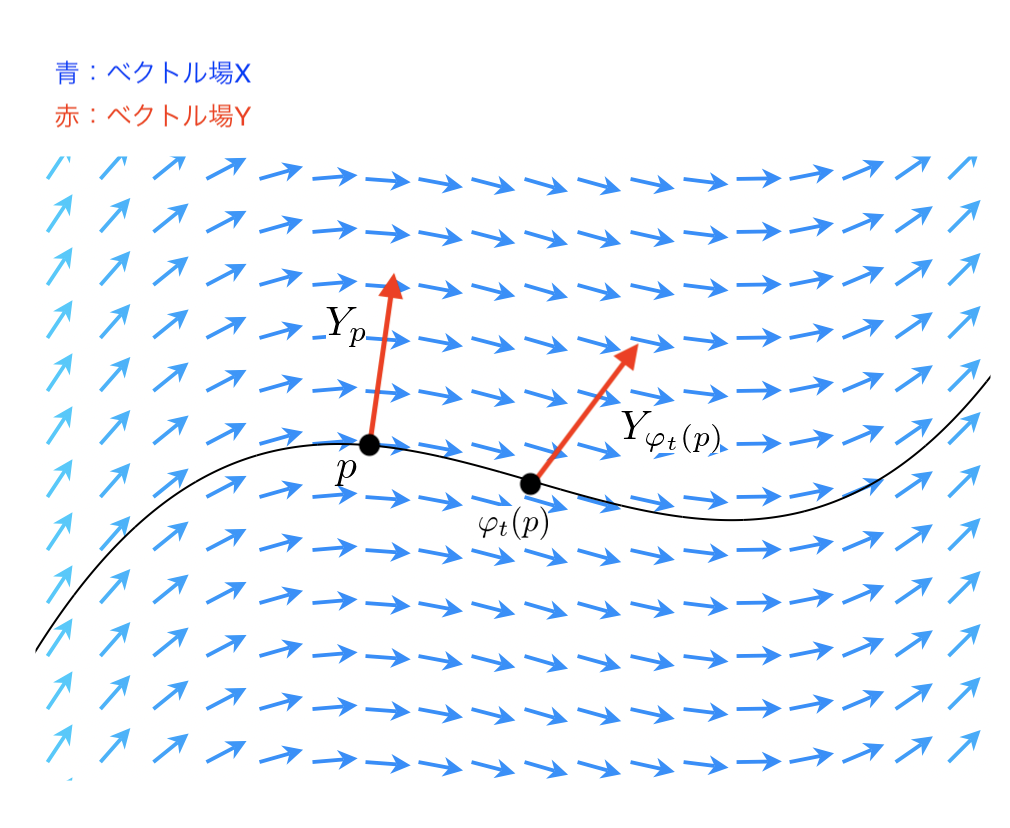
$X, Y$ を $M$ 上のベクトル場としたとき、$Y$ の $X$ によるリー微分は、各点 $p$ での $Y_p$ と $Y_{\varphi_t(p)}$ との差の極限として定義される ($\varphi_t$ は $X$ が定めるフローである)。しかし、$p$ と $\varphi_t(p)$ は異なる点のため、比較できない。従って、フローの微分を用いて同じ点に移す。$p$ に移す方法と $\varphi_t(p)$ に移す方法があるが、前者を採用する (結果はどちらでも同じである)。つまり、$Y_{\varphi_t(p)}$ を $(\varphi_{-t})_*$ によって $p$ 上の接ベクトル空間に移す。
定義. リー微分
$Y$ の $X$ によるリー微分 $L_X Y$ を
$$L_X Y = \lim_{t \to 0} \frac{(\varphi_{-t})_*(Y) – Y}{t}$$
と定義する。$\Box$
リー微分は括弧積 $[X, Y] (=XY – YX)$ と一致する。これを確認しよう。ベクトル場が一致することを示すには、任意の関数 $f \in C^{\infty}(M)$ への作用が一致することを示せば良い。まず、
$$(\varphi_{-t})_*(Y)f = Y(f \circ \varphi_{-t}) \circ \varphi_{t} = \varphi_{t}^*(Y(f \circ \varphi_{-t}))$$
である (ここで、$g \in C^{\infty}(M)$ に対して $\varphi_{t}^*(g)$ は $g \circ \varphi_{t}$ をあらわす)。よって、
\begin{align} (\varphi_{-t})_*(Y)f -Yf &= \varphi_{t}^*(Y(f \circ \varphi_{-t})) -Yf \\ &= \{\varphi_{t}^*(Y(f \circ \varphi_{-t})) -\varphi_{t}^*(Y(f))\} + \{\varphi_{t}^*(Y(f)) -Yf\} \\ &= \varphi_{t}^*(Y(f \circ \varphi_{-t} -f)) + \{\varphi_{t}^*(Y(f)) -Yf\} \\ \end{align}
であり、1項目 (を $t$ で割ったもの) は $Y(-X)f$ に収束、2項目は $X(Yf)$ に収束するから、リー微分は
$$Y(-X)f + X(Yf) = XYf -YXf = [X, Y]f$$
に一致する。補足すると、$Yf$ は普通のベクトル場の作用、$\varphi_{t}^*(Y(f))$ は $Yf$ のフローで流れた点 $\varphi_{t}(p)$ での値、$\varphi_{t}^*(Y(f \circ \varphi_{-t}))$ は $f$ をフローで流した関数に $Y$ を作用させたものの、$\varphi_{t}(p)$ での値である。証明は微分形式の幾何学に従った。
リー微分は微分同相から同型が誘導されるもの (微分形式やテンソルなど) であれば同様に定義できる。また、普通の方向微分と違い、リー微分の各点 $p$ での値は $X$ の $p$ の近傍の値に依存することに注意されたい。これは $YX$ の項があることから想像できると思う。
接続について
次は接続について。接続は方向微分を一般化したものといえる。しかし、冒頭で確認したように、方向微分を素直に実行すると座標変換でうつり合わない。もっと素朴に、滑らかな曲線 $c: [0, 1] \to M$ に対し、 $\frac{d}{dt}|_{t=0}X(c(t))$ と定めてみよう。このままでは、$t_0 \neq t_1$ ならば $X(c(t_0))$ と $X(c(t_1))$ は別の空間にあるため比較できない。そこで、なんでも良いので曲線に沿った接空間の同型があったとして、微分をどう定められるかを考えてみる。
とりあえず次のようなものを考えよう。多様体 $M$ 上の任意の滑らかな曲線 $c$ に対して、線型写像$P(c)^{s}_{t} : T_{c(t)}M \to T_{c(s)}M$ が定まり、以下の性質を満たすとする。
- $P (c)^{s}_{s} = \mathrm{Id}$
- $P (c)^{s}_{t} \circ P(c)^{t}_{u} = P(c)^{s}_{u}$
- $P(c)^{s}_{t}$ は $s, t$ に対して滑らか
$P(c)^{s}_{t} \circ P (c)^{t}_{s} = P(c)^{s}_{s} = \mathrm{Id}$ だから、任意の $s, t$ に対して $P(c)^{s}_{t}$ は全単射である。これによって、曲線上の別の点の接空間にあるベクトル同士を比較できる。
$Y$ をベクトル場とする。以下の微分
$$\frac{d}{dt}P(c)^{t_0}_{t}(Y(c(t)))|_{t = t_0} = \lim_{t \to t_0} \frac{P (c)^{t_0}_{t}(Y(c(t)) – Y(c(t_0))}{t}$$
を考える。$Y(c(t)) = \sum_{i}Y_i(c(t))\frac{\partial}{\partial x_i}$とし、$P(c)^{t_0}_{t}((\frac{\partial}{\partial x_i})_{c(t)}) = e_i(t) \in T_{c(t_0)}M$ とおくと、$P (c)^{t_0}_{t}(Y(c(t))) = \sum_{i} Y_i(c(t)) e(t)$ と書ける。従って、上記の微分は
$$ \frac{d}{dt}P(c)^{t_0}_{t}(Y(c(t))) = \sum_{i} \frac{dY_i(c(t))}{dt}e_i(t) + \sum_{i} Y_i(c(t)) \frac{de_i(t)}{dt}$$
となる。冒頭で計算したような方向微分では、右辺2項目にあるベクトルの微分を考慮していなかったが、上記の計算ではそこが考慮されている。これを念頭に接続の定義を見てみよう。(ちなみに、話の流れ上 $P$ を用いたが、同様の性質を満たすものを接続を用いて改めて定義するので、これ以降は忘れてしまってよい。)
定義. 接続
$M$ を多様体とし、 $\chi(M)$ を $M$ 上の滑らかなベクトル場全体の集合とする。
$$\nabla: \chi(M) \times \chi(M) \to \chi(M); (X, Y) \mapsto \nabla_X Y$$
が以下の条件を満たすとき、$\nabla$ を $M$ 上の接続という。
- $\nabla_X (Y + Z) = \nabla_X Y + \nabla_X Z$
- $\nabla_{(X + Y)} Z = \nabla_X Z + \nabla_Y Z$
- $\nabla_{fX} Y = f\nabla_X Y$
- $\nabla_{X} (fY) = (Xf)Y + f\nabla_X Y$
ただし、$f \in C^{\infty}(M), X, Y, Z \in \chi(M)$ である。$\Box$
接続を方向微分の一般化だと思えば、1, 2, 3 は納得いくだろう。4の右辺2項目がベクトルの微分に関する項であり、冒頭で述べた方向微分と唯一異なる点である。この部分を適当な座標系のもと、紐解いてみよう。$X = \sum_i X_i \frac{\partial}{\partial x_i}, Y = \sum_i Y_i \frac{\partial}{\partial x_i}$ とすると、
$$\nabla_X Y = \sum_{i,j} X_i \frac {\partial Y_j}{\partial x_i} \frac{\partial}{\partial x_j} + \sum_{i, j} Y_j X_i \nabla_{\frac{\partial}{\partial x_i}} \frac{\partial}{\partial x_j}$$
だから、不明なのは $\nabla_{\frac{\partial}{\partial x_i}} \frac{\partial}{\partial x_j}$ の部分のみである。この部分の $k$ 成分の値を $\Gamma_{i, j}^{k}$ とおけば、$\nabla_{\frac{\partial}{\partial x_i}} \frac{\partial}{\partial x_j} = \Gamma_{i, j}^{k} \frac{\partial}{\partial x_k}$ と表される。不明であることに変わりはないが、$\Gamma_{i, j}^{k}$ が決まれば接続が決まるということはわかる。(ちなみに、接続の値域がなめらかなベクトル場であることから、$\Gamma_{i, j}^{k}$ は滑らかな関数になる。)
平行移動
接続は、ある接ベクトル $v$ がある方向にちょっと動いた時に、$v$ がどう動くかを決めているといえる (値としては、その動くべき方向と実際の値のズレが与えられる)。従って、曲線 $c$ とその曲線上のある点での接ベクトルが与えられた時、曲線の接線方向の接続の値が常に $0$ になるようなベクトル場を見つけられれば、そしてそれがただ一つであれば、その曲線に沿って接ベクトルを動かす事ができたといえる。
それが実際に可能であることは、$\nabla_{\dot{c}(t)} X = 0$ が $X$ を未知関数とする微分方程式であることと、微分方程式の解の存在と一意性からわかる。そのようにして得られる写像
$$\Pi^{\nabla}(c)_{t_0}^{t} : T_{c(t_0)}M \to T_{c(t)}M$$
を $c$ に沿った平行移動と呼ぶ。$\nabla$ の線形性から、$\Pi^{\nabla}(c)_{t_0}^{t}$ が線形写像である事がわかる。また、ベクトル場のフローが $\varphi_s \circ \varphi_t = \varphi_{s+t}$ を満たすことと同様の議論で、
- $\Pi^{\nabla} (c)^{s}_{s} = \mathrm{Id}$
- $\Pi^{\nabla} (c)^{s}_{t} \circ \Pi^{\nabla}(c)^{t}_{u} = \Pi^{\nabla}(c)^{s}_{u}$
が成り立つことがわかる。$s, t$ について滑らかであることは $\Gamma_{i, j}^{k}$ が滑らかであることから明らかである。
$P$ と同様の方法で $\Pi^{\nabla}$ を用いて微分すると、それは接続と一致する。証明はそれほど難しくない。
$T_{c(t_0)}M$ の基底 $e_1(0), \dots, e_n(0)$ を適当に選び、
$$e_i(t) = \Pi^{\nabla}(c)_{t_0}^{t}(e_i(0))$$
とおくと、$e_1(t), \dots, e_n(t)$ は $T_{c(t)}M$ の基底になる。従って、ベクトル場 $Y$ に対し、$c$ 上の関数 $Y_i(t)$ が存在して、
$$Y(c(t)) = \sum_i Y_i(t) e_i(t)$$
と表される。定義から
$$\Pi^{\nabla}(c)_{t}^{t_0}(Y(c(t))) = \sum_i Y_i(t) e_i(0)$$
である。これの微分と $\nabla_{\dot{c}(t_0)} Y$ が一致することを示せばよいが、基底の取り方からどちらも $\sum_i \frac{dY_i}{dt}e_i(0)$ である。
まとめ
ストーリーとしては平行移動から入って接続を説明する方がわかりやすいと思うのだが、理論上は接続を先に定義する方がシンプルである。ストーリー重視で平行移動から定義してみようと思ったが、正確な定義がよくわからなかったので、差し当たり必要な性質だけで話を作って、平行移動の正確な定義は通常どおり接続を用いることにした。リー微分と比較すると、フローの作り方が異なるために意味合いや性質が異なるが、フローで流すというテクニカルな点では共通しているところが面白い。
参考文献
[1] 森田茂之. 微分形式の幾何学
