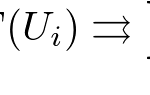ブローアップは複素幾何学や代数幾何学で良く用いられる操作です。分かってしまえば案外簡単なのですが、何をしようとしているかわからないと混乱しがちなので、もっとも簡単な実平面の場合の解説をします。実多様体論では使われることは少ないですが、4次元トポロジーを勉強すると、複素曲面の例と絡めて沢山でてくるので、知っておいて損はないと思います。統計学でもブローアップが使われます*1。
特異点解消
特異点解消の定義はしませんが、差し当たり、下図の様な曲線の交差をほどくことだと思ってください。その際、ほどけた曲線を別の空間に実現させても構いません。少し詳しく書くと、特異点を持つ曲線を $C \subset \mathbb{R}^2$ としたとき、ある空間 $W$ とその中の曲線 $\tilde{C} \subset W$ と写像 $\pi : W \to \mathbb{R}^2 $ で、$\pi(\tilde{C}) = C$ かつ特異点を除いた部分で同型となるものを構成するということです。正確な定義はちゃんとした教科書を参照してください (例えば[2])。
今の例では、右上から左下に向かう部分と、左上から右下に向かう部分を区別できれば十分です。この2つの違いは原点への入り方です。だから、原点での接線で点を区別できれば上手くいきそうです。ここで、射影空間の点と空間上の直線は1:1に対応するのでした。従って、「原点を射影空間で置き換えて」、原点への入り方 (=接線)と対応する射影空間の点で曲線をくっ付け直すことで、交差をほどくことができそうです。
射影空間と普遍線束
射影空間のおさらいをしましょう。射影空間 $\mathbb{RP}^n$ は $\mathbb{R}^{n+1}$ の原点を通る直線全体の集合でした。原点を通るある直線上の、原点以外の点は、適当な $c \in \mathbb{R} \setminus \{0\}$ をかけることで移り合います。従って、
$$\mathbb{RP}^n := (\mathbb{R}^{n+1} \setminus \{0\}) / \sim$$
と定義します。ただし、同値関係は定数倍で移り合うとき同値としました。位相は商位相を入れます。直感的に、近い直線は近いと思って問題ありません。$\mathbb{RP}^1$ を図示すると、以下の様に円周の下半分を切り取って、端と端をくっ付けた形になります。次元が$1$の場合は円と同相になりますが高次元では状況は異なります。
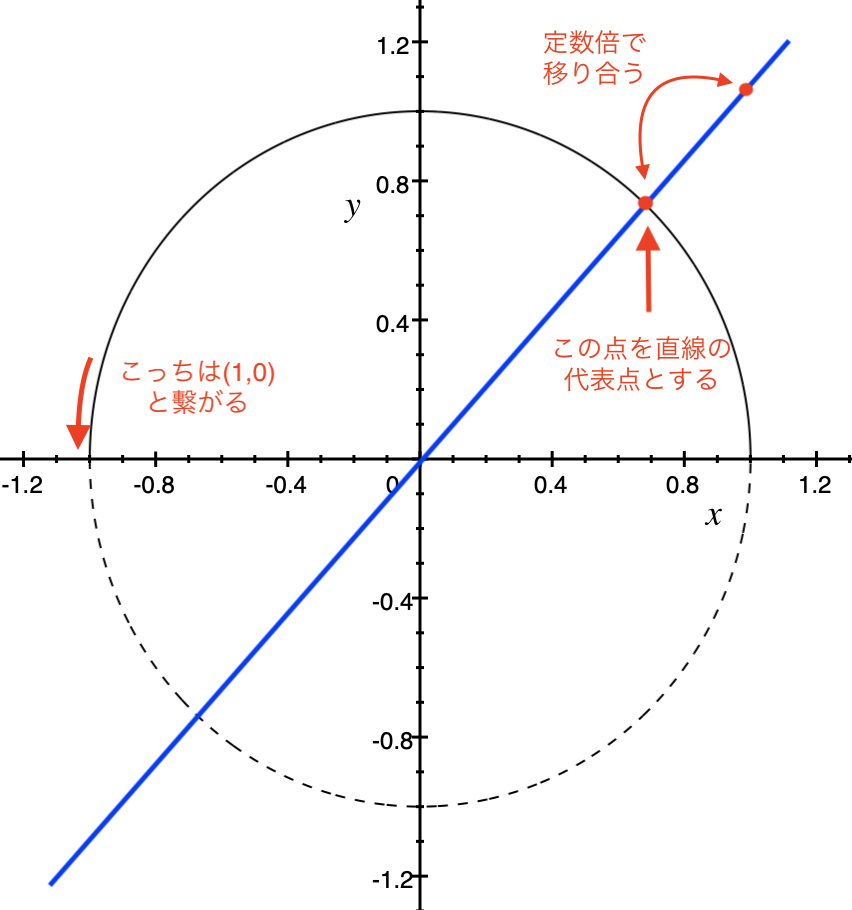
射影空間上の普遍線束 $L$ を $\mathbb{RP}^n \times \mathbb{R}^{n+1}$ の部分集合
$$ L := \{ (p, x) \mid p \in \mathbb{RP}^n, x \textrm{ は } p \textrm{ に対応する } \mathbb{R}^{n+1} \textrm{ の直線上の点 }\}$$
として定義します。$n=1$ の場合は $L$ は次の様な空間になります。上図の半円を $(1, 0)$ から反時計回りに $(-1, 0)$ まで動くと、対応する直線は、直線としては一致しますが、±が逆転します。つまり、端と端をひねって張り合わせた、メビウスの帯のような形になります。ただし、メビウスの帯と違って、帯の幅が無限に伸びています。
ブローアップ
本題のブローアップです。引き続き $n=1$ とし、先程の $L$ を $\mathbb{R}^2$ に射影してみましょう。つまり、$(p, x)$ に対して $x$ を対応させます。この写像は全射になります。なぜなら、$\mathbb{R}^2$ の任意の点に対して、その点を通る直線が存在するからです。また、原点を除いて単射であることも簡単にわかります。さらに、全ての直線が原点を通るので、$0$ の逆像が $\mathbb{RP}^1$ になることもわかります。以上のことから、$L$ は $\mathbb{R}^2$ の原点を $\mathbb{RP}^1$ に置き換えたものであることがわかります。従って、$L$ が求めようとしていた空間なのでした。
これだけだと本当に交差が外れるのか分かりづらいので、もう少しちゃんと書きましょう。
$p \in \mathbb{RP}^1$ を $[p_0 : p_1]$ の様に、比で表します。$\forall c \neq 0 \in \mathbb{R}$ に対して$[p_0 : p_1] = [c p_0 : c p_1]$ が成り立ちます。また、$p_0$, $p_1$ の少なくとも一方は $0$ ではありません。$L$ は $\mathbb{RP}^1 \times \mathbb{R}^2$ 上の代数方程式の零点集合
$$\{(p, x) \mid p_0 x_1 -p_1 x_0 = 0, \ p \in \mathbb{RP}^1, \ x \in \mathbb{R}^2\}$$
で表されます。これは$x$ が $p$ に対応する直線に含まれているという条件のみからわかります。$p_0 \neq 0$ のときに、$s = \frac{p_1}{p_0}, t = x_0$ とおくと、$x_1 = s t$ が成り立つから、$(s, t)$ から $L$ の元が一意的に定まります。$p_1 \neq 0$ のときも同様に $u = \frac{p_0}{p_1}, v = x_1$ とおくと、$(u, v)$ から $L$ の元が一意的に定まります。
$y^2 = x^3 + 2x^2$ をブローアップして、$(x_0, x_1)$ を $(x, y)$ と置き直して、$(s, t)$ で表してみましょう。計算するとそれは $(s t)^2 = t^3 + 2 t^2$ なります。整理して、
$$t^2(s^2 – t – 2) = 0$$
となります。$t^2 = 0$ が表す曲線は $\mathbb{RP}^1$ ですので、今回はこの部分を考えないことにします。$s^2 – t – 2$ が表す曲線は元の曲線と対応します。それは $(s, t)$ を $(x, y)$ で書き直すとわかります。交差が外れているかを確認するには、$t = 0$ のときの $s$ の値を求めれば良いのですが、それは $\pm \sqrt{2}$ ですので、期待通りふたつ存在し、交差が外れていることがわかります。$(u, v)$ で置き換えても期待通りの結果が得られるはずです。
$s$ は定義から傾きに等しいので、特に原点では接線の傾きと等しくなるはずです。$y$ について解くと、$y = \pm x \sqrt{x + 2}$ となりますが、$+$ の方は右上から左下に向かう部分、$-$ の方が左上から右下に向かう部分です。原点の微分の値を計算すると、それぞれ $\sqrt{2}, -\sqrt{2}$ であることがわかるので、やはり期待通り、原点への入り方で点を区別できていることがわかりました。
おまけ
$\mathbb{RP}^1$ 上の普遍線束 $L$ は、メビウスの帯の様な空間になるのでした。$\pi: L \to \mathbb{RP}^1$ を自然な射影とすると、これは直線束になります。$\mathbb{RP}^1 \simeq S^1$ だったので、$L$の切断は $L$ のループになります。また、$L$ の切断は必ず $0$ 切断と交わります。これは、$0$ と交わらないように切断を伸ばして行ったときに、1周すると符号が逆転してしまうことからわかります。切断ではなくなってしまいますが、2周すれば$0$と交わらない様にループを作ることができます。
さて、$L$ をリーマン面の構成のように、無限遠に点を加えてコンパクト化します(実はこれは $\mathbb{RP}^2$ になります)。2週したループは $\mathbb{RP}^1$ とは交わらないため、$\mathbb{RP}^1$ を除いた
$$ L \cup \{\infty \} \setminus \mathbb{RP}^1 = \mathbb{R}^2 \cup \{\infty \} \setminus \{0\}$$
上のループと思えます。これは一点に縮めることができます。もし、1周しかしていないループが一点に縮められないなら、基本群が $\mathbb{Z} / 2\mathbb{Z} $ の空間が構成できたことになります。これについてはファン・カンペンの定理を用いれば示せると思います。
以上、おまけでした。
参考文献
[1]. 渡辺澄夫 代数幾何と学習理論 (知能情報科学シリーズ)
[2]. 堀川穎二 新装版 複素代数幾何学入門 (岩波オンデマンドブックス)
[3]. 小林昭七 複素幾何
