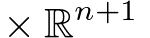数学では張り合わせによって数学的対象を構成することがよくあります。多様体はその典型的な例です。層は、張り合わせによる構成をとにかく一般化した概念であるといえます。層の定義するのに、まず前層が定義されますが、これらの差は分かりづらいように思います。そこで、前層で層でないものの例を挙げてこれらを解説しようと思います。
前層と層の定義
定義. 前層 (presheaf)
$X$ を位相空間とする. $\mathbf{Open}(X)$ を $X$ の開集合を対象とし, 包含写像を射とする圏とする. $\mathbf{Open}(X)^{op}$ から集合の圏 $\mathbf{Set}$ への関手を $X$ 上の前層という. $\Box$
$F$ を $X$ 上の前層とします。このとき $s \in F(U)$ を $F$ の $U$ 上の切断といいます。$F$ は$\mathbf{Open}(X)^{op}$ からの関手なので、開集合の包含 $\iota: V \to U$ に対し矢印の向きが逆になり、$F(\iota): F(U) \to F(V)$ が対応します。$F(\iota) = \rho^{U}_{V}$ とおきます。また、$\rho^{U}_{V}(s) = s|_{V}$ と関数の制限のように書くこともあります。
定義. 層 (sheaf)
$X$ を位相空間, $F$ を $X$ 上の前層とする. 任意の開集合 $U$ とその被覆 $\{U_i\}_{i \in I}$ に対して以下の図式が equalizer であるとき, $F$ を層という.
$$ F(U) \rightarrow \prod_{i \in I} F(U_i) \rightrightarrows \prod_{i, j} F(U_i \cap U_j)$$
ただし, 最初の矢印は $U_i \to U$ に対応する射, 2つ目の矢印は $U_i \cap U_j \to U_i$ と $U_i \cap U_j \to U_j$ に対応する射である. $\Box$
equalizer であるという条件は以下のように言い換えられます。equalizer であることから、最初の矢印は単写です。よって、
- $s, t \in F(U)$ が全ての $i \in I$ について $s|_{U_i} = t|_{U_i}$ を満たすならば、$s = t$である。
となります。また、$\{s_i\}_{i \in I} \in \prod_{i \in I} F(U_i)$ が $\prod_{i, j} F(U_i \cap U_j)$ への 2 つの写像で一致することは
$$s_i |_{U_i \cap U_j} = s_j|_{U_i \cap U_j}$$
を意味し、equalizer の普遍性からある $s \in F(U)$ からくるので、
- $s_i \in F(U_i) \ (i \in I)$ で $s_i |_{U_i \cap U_j} = s_j|_{U_i \cap U_j}$ を満たすものは $s \in F(U)$ から来る。
となります。つまり層は、局所的に同じであれば同じ、かつ局所的に同じものは張り合わせることができるものであると言えます。
層でない前層
層でない前層は、局所切断を張り合わせたものが切断にならないことがある (拡張が存在しない) か、局所的に同じなのに異なる切断が存在する(拡張の一意性を満たさない) のどちらかです。これらの例を挙げます。
1. $\mathbb{R}$ 上の有界関数のなす前層
$f(x) = x^2$ は各 $U_i = (i -1, i + 1)$ $(i \in \mathbb{Z})$ 上で有界ですが、$\mathbb{R}$ 上では有界ではありません。よって局所切断を張り合わせたものが $\mathbb{R}$ の切断になりません。
2. $\mathbb{R}$ 上の距離関数のなす前層
$U \subset \mathbb{R}$ に対し、$F(U)$ を $U$ 上の距離関数の集合とします。$\rho$ を距離関数の制限で定めると、$F$ は $\mathbb{R}$ 上の前層となります。しかし、$U$ 上の距離 $d_U$ と $V$ 上の距離 $d_V$ で $U \cap V$ 上で一致するものがあったとしても、$x \in U \setminus V$, $y \in V \setminus U$ 間の距離はそれらの情報から一意に定まりません。従って、局所的に同じだが、異なる切断が存在します。
参考文献
[1] R.ハーツホーン. 代数幾何学 1
[2] S.マックレーン. 圏論の基礎
