統計的推定は、与えられたデータからその裏にある法則を見出すための手法です。しかし実は、与えられたデータのみでは推定を行うことはできず、必ずいくつかの仮説、仮定を必要とします。そして、いくつかの仮定をすれば、推定は具体的な手続きに落とし込まれます。
機械学習について勉強するとき、最小二乗法はおそらく最初に出会う推定方法でしょう。最小二乗法は誤差の二乗が最小になるものを選択するという手続きです。しかしながら、それが統計的な推定を行う上でどのような意味があるのか、どのような仮説のもとでこの手続きが導かれたのか、という説明は多くの場合されません。
一般に、推論の手続きだけを見て、どのような仮説から導かれたのか逆算するのはとても難しいです。つまり、なぜ二乗なのかを考えても、その仮説に辿り着くことはできません。従って、統計を勉強するときは推論の手続きだけでなく、どのような仮定のもとにその手続きを得られたのかを併せて勉強することがとても重要です。
本記事では、なぜ最小二乗法を用いるのか、どのような仮説の元にその手続きに至ったのかを解説しようと思います。
回帰分析と3つの仮定
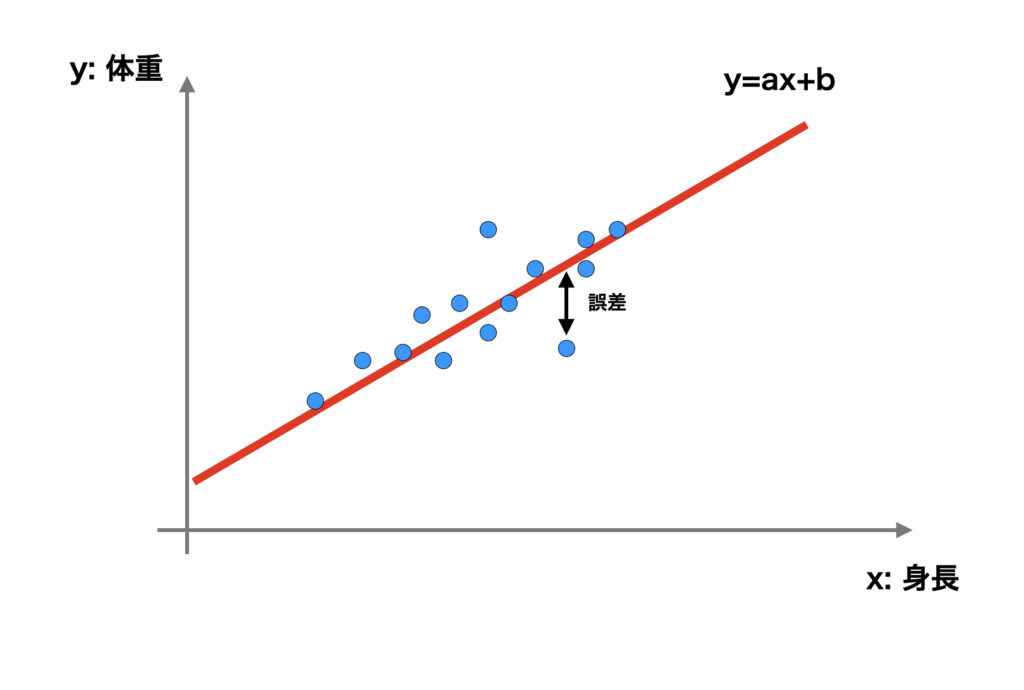
最小二乗法がよく使われるケースとして回帰分析があります。回帰分析というのは、例えば体重と身長のような、2種のデータ $x$, $y$ のペア $\{(x_1, y_1), \cdots, (x_n, y_n)\}$ が与えられたとき、$x$ と $y$ の関係を推定する手法です。
最小二乗法というのは、$x$ と $y$ はおおよそ直線的 (例えば $y = ax + b + $ 誤差 のよう) な関係性もつと仮定して、誤差の2乗の和 $\sum_{i = 1}^{n} (y_i -(ax_i +b))^2$ を最小とする $a$, $b$ を求めることでした。そしてそれが、$x$ と $y$ の関係を最も良く表しているとするのでした。
ここでは最小二乗法の代わりに、以下のような仮定をします。
- $x$ と $y$ はおおよそ直線的である。つまり、$y = ax + b + \varepsilon$ と表すことができる。$\varepsilon$ は誤差を意味する。
- その誤差は正規分布に従って分布している。
- 最尤推定を用いればうまく推定できる。
誤差の2乗の最小化するという部分が、仮定 2. 3.に置き換わっています。上記の3つの仮定から最小二乗法が導かれることを説明します。
1.と2.から、$x$ と $y$ の関係は条件付き確率密度関数で表現できます。誤差 $\varepsilon$ が正規分布なので、以下のようになります。
$$ p(y | x) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{{(y \ -(ax +b))^2}}{2\sigma^2}\right) $$
右辺は $ax + b$ を中心、$\sigma > 0$ を分散とする正規分布です。$a$, $b$ は未知のパラメーターです。
3.の最尤推定を用いて $a$, $b$ を決定することで、推定が完了します。最尤推定は、データ $\{(x_1, y_1), \cdots, (x_n, y_n)\}$ が得られる確率 (正確には確率ではありません。尤度と呼びます。) を最大にする $a$, $b$ を採用するという方法です。つまり、以下の値
$$ \prod_{i = 1}^{n} p(y_i | x_i) = \prod_{i = 1}^{n} \frac{1}{\sqrt{2\pi}\sigma} \exp\left(-\frac{{(y_i \ -(ax_i +b))^2}}{2\sigma^2}\right)$$
を最大にする $a$, $b$ を決めるということです。右辺の対数を取ると (対数関数は単調増加関数なので、対数をとっても問題ありません。)
$$ -n \log(\sqrt{2\pi} \sigma) \ -\frac{\sum_{i = 0}^{n} (y_i -(ax_i +b))^2}{2\sigma^2}$$
となります。式を眺めると、尤度を最大化する $a$, $b$ は $\sigma$ の値によらず $\sum_{i = 0}^{n} (y_i -(ax_i +b))^2$ を最小化する $a$, $b$ と一致します。これで最小二乗法と誤差を正規分布とした最尤推定に一致することがわかりました。
補足とまとめ
回帰分析を例に、最小二乗法が3つの仮定の上に成り立っていることを説明しました。その3つの仮定について、簡単に補足します。
まず 1番目の仮定、$x$ と $y$ が直線的な関係であることについて補足します。これについては、$x$ と $y$ が直線的でない場合も考えることができます。例えば $x$ を $y$ の2次以上の多項式と仮定することができます。そうするとより複雑な関係性を推定できることがあります。
次に2番目の、誤差が正規分布であるという仮定は、例えば外れ値が多い場合や、誤差が必ず0より大きいことがわかっている場合など、正規分布に従っていないことが明らかな場合は別の分布を選んだほうが良いことがあります。そうすると、誤差の2乗ではなく、別の評価をすることになります。例えば誤差をラプラス分布と仮定すると、誤差の絶対値の和を最小化することになります。
最後に3つ目の仮定の最尤推定は、”尤度を最大化するパラメーターを選ぶ” という手続きに過ぎません。ですので、この記事の解説は、最小二乗法という手続きを最尤推定というより汎用的な手続きに置き換えたということになります。そしてそれによって、誤差が正規分布であるという仮定が浮き彫りになりました。
ここで注意したいのが、推定の手続きを行う際、この3つの仮定の “妥当性には何も言及していない” ということです。$x$ と $y$ の関係が直線的である理由もなければ、誤差が正規分布に従っていると思える理由もなければ、最尤推定でうまく推論できる保証もありません。
統計的推論は仮定の妥当性に関係なく手続きに落とし込むことができてしまいます。これは統計的推論の大きな長所ではありますが、その一方で、その手続きによって、一見すると客観的で科学的な推論が行われたと錯覚してしまいます。これはとても恐ろしいことです。
仮定が妥当でなければ、推論結果の正しさは論理的には保証されません (経験的に保証されることはある)。しかし、仮定の妥当性の判定は統計学の (一般論の) 範囲外であり、具体的な状況に基づいて判断するしかありません。もし統計的に判断しようとすれば、その判断のための新たな仮定が必要になり、新たな仮定の妥当性を統計的に判断するためには、さらに新たな仮定が必要になります。
改めてこの記事で述べたことの意義を考えると、誤差の2乗を最小化するという見方よりも、誤差が正規分布であるという見方の方が、仮定の妥当性を考える上でより理解しやすいということです。先ほども述べましたが、外れ値が多い場合や誤差に特徴がある場合、推論がうまくいかなかったとしても、誤差の2乗を最小化するという見方ではその原因がわかりません。一方で、誤差を正規分布と仮定する、という見方であれば、誤差が正規分布に従っていないからうまくいかないのだと判断することができます。
最後に、最尤推定はどのような仮定のもとに得られた手続きなのか、という疑問が残っています。最尤推定はほとんどの統計的推論で用いられる手法なので、それを知ることは統計的推論を理解する上で非常に重要なことです。これについては以下の記事で解説しています。数学的に難しいところがあるかもしれませんが、その部分は読み飛ばしても理解できるように書いたつもりです。興味がある方はご一読ください。
