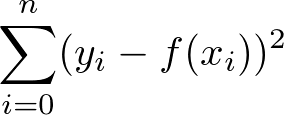機械学習を勉強すると、必ず統計学についても学ぶことになります。そして、多くの場合それらの関係性が明示されることはないように思います。解析手法に焦点を当てれば、どちらも同じことをやっているので違いがないように思います。しかし、教師あり、教師なし学習という概念は統計学にはありませんし、一方で点推定と区間推定という概念は機械学習においてそれほど話題になりません。それゆえ、大体同じものだけど、なんか違うんだろうなという印象をお持ちの方も多いと思います。
そこで本記事では、数学的な枠組みの観点でそれらについての理解を目指しつつ、両者の違いについての個人的な見解を述べたいと思います。
※ この記事では確率分布と確率密度関数を区別せず書いていますが、正確には異なるものです。
目次
統計的推定とは
まずは統計的推定の枠組みについて説明します。統計的推定の問題設定は基本的に以下のようなものです。
- データ $\{x_1, \dots, x_d\}$ が与えられいる。
- それらは $X$ ($= \mathbb{R}^n$ であることが多い) 上のデータである。
- そして、データ $x_1, \dots, x_d$ は $X$ 上の未知の確率分布 $q(x)$ に従って独立にサンプリングされたと考える。
上記のような状況で、未知の分布 $q(x)$ が何であるかを突きとめる、というのが目標です。しかし、この設定だけでは $q(x)$ の候補が多すぎるため決定できません (データを無限個得られるならば $q(x)$ を決定できますが、現実的にはあり得ません)。そこで、候補となる確率分布に制限をつけ、それを確率モデルと呼びます。
確率モデルとは
確率モデルは、パラメーター空間 $W$ ($\subset \mathbb{R}^m$ であることが多い) から $X$ 上の確率分布全体の空間 $\mathcal{P}(X)$ への写像 $\tau : W \to \mathcal{P}(X)$ で与えられます。例えば、$X = \mathbb{R}$ とし、正規分布を確率モデルとする場合は、
$$W = \{ (m, \sigma) \in \mathbb{R}^2 \mid \sigma > 0 \}$$
$$\tau(m, \sigma) := \frac{1}{\sqrt{2 \pi \sigma}} \exp \left( -\frac{(x -\mu)^2}{2 \sigma} \right)$$
となります。
確率モデルを決めた後は、$\tau(W) \subset \mathcal{P}(X)$ の中で $q \in \mathcal{P}(X)$ に最も “近い” と思われるものを決定します。なぜ “一致する” ではなく “近い” なのかというと、一般には $q \in \tau(W)$ を仮定できないからです。
$X$ が有限集合であれば、$X = \{x_1, \dots, x_m\}$ 上の任意の確率分布は $\sum_{i=1}^m p_i = 1$ を満たす正数 $p_i$ により表すことができるので、$q \in \tau(W)$ を仮定できます。一方 $X$ が無限集合の場合、正規分布やディリクレ分布のような、シンプルな数式で表される分布を用いることが一般的ですが、$q$ がそのような分布で表されることが期待できない場合があります。あるいは、複雑な確率モデルで表現できたとしても、推論に十分なデータが足りないということがあります。その場合でも $q$ を近似的に求めることに意味があるので、$q \notin \tau(W)$ の状況でも取り敢えずの答えを得られる枠組みが必要です。
そのとき、以下が問題になります。
- 確率分布の近さをどう定めるか。
- $q$ は未知なので、直接 $q$ との近さを測ることができない。
- 他の確率モデルで得られた推論結果との比較できるのか。
1番目について、確率分布の近さについては多くの場合尤度、あるいはKLダイバージェンスが用いられます。これは後ほど解説します。2番目については、いつか別の記事で考察できたらいいなと思っています。3番目は別の記事で解説する予定です。
近さの尺度としての尤度とKLダイバージェンス
$p(x, w) := \tau(w)(x)$ とおきます。尤度 $L(w)$ は以下で定義されます。
$$L(w) = \prod_{i=1}^d p(x_i, w)$$
$\tau(w)$ が未知の分布 $q$ に近ければ、各項 $p(x_i, w)$ が大きくなる可能性が高いので、 $L(w)$ が大きくなる可能性が高くなります。この尤度をパラメータ $w$ のデータ $\{x_1, \dots, x_d\}$ への当てはまりの良さの指標とし、$L(w)$ を最大化する $w$ に対応する分布 $\tau(w)$ を推定の答えとする方法を、最尤推定と呼びます。
しかし、尤度では “確率分布の近さ” というニュアンスはありません。そこで、$p_1, p_2 \in \mathcal{P}(X)$ に対しKLダイバージェンス (カルバック・ライブラー情報量) を以下で定義します。
$$ KL(p_1 || p_2) = \int_X p_1(x) \log \frac{p_1(x)}{p_2(x)} dx$$
KLダイバージェンスは、分布 $p_1$ を分布 $p_2$ と偽ったときにバレる速さを表しています (これについては別の記事で解説する予定です)。バレるのが遅いほど “確率分布が近い” と解釈できます。
KLダイバージェンスと尤度の関係をみてみましょう。$KL(q(x) || p(x, w))$ を計算すると、
\begin{align} KL(q(x) || p(x, w)) &= \int_X q(x) \log \frac{q(x)}{p(x, w)} dx \\ &= \int_X q(x) \log q(x) dx \ -\int_X q(x) \log p(x, w)dx \end{align}
となります。第1項は定数であり、第2項について、$\tilde{q}(x) = \frac{1}{d}\sum_{i=1}^d \delta_{x_i}(x)$ とおいたとき、大数の法則から
$$\lim_{d \to \infty} -\int_X \tilde{q}(x) \log p(x, w)dx = -\int_X q(x) \log p(x, w)dx$$
を満たし、
\begin{align} -\int_X \tilde{q}(x) \log p(x, w)dx &= -\frac{1}{d}\sum_{i=1}^n \log p(x_i, w) \\ &= -\frac{1}{d} \log L(w) \end{align}
は尤度の対数の $ -\frac{1}{d}$ 倍です。よって尤度を最大化することは、近似的に $q$ と $p(x, w)$ のKLダイバージェンスの最小化をしていることになります。
確率分布の近さの尺度としてKLダイバージェンスの他に、Wasserstein距離を用いることがあります。Wasserstein距離については別の記事で解説する予定です。
基本的な方針として、尤度が大きいパラメーターを選ぶというのは正しいと思いますが、尤度が最大であるパラメーターが一番良いとは限りません。$\tau$ が単射でない場合は、尤度が最大のパラメーターがサンプルデータに対して不安定なことがあるようです。その場合は、尤度が最大のパラメーターを選択するのではなく、尤度で平均をとる方法があります。尤度の $W$ での積分が有限にならない場合があるので、$W$ 上の確率分布 $\varphi(w)$ (事前分布と呼ぶ) をうまく取り、$Z = \int_W L(w) \varphi(w) dw$ が有限の値をとるようにします。このとき、
$$p^*(x) = \int_W p(x,w) \frac{L(w) \varphi(w) }{Z} dw$$
を答えとします。これをベイズ推定と呼びます。
機械学習と統計的推定の違い
機械学習と統計的推定は、どちらもサンプルから未知の分布を推定することを目標としており、数学的には全く同じものであると言えます。しかし、機械学習では教師あり学習、教師なし学習という分類がある一方で、統計学ではこのような分類に対応するものはありません。これについて考えてみましょう。
教師あり学習と教師なし学習
教師あり学習と教師なし学習の違いは、推定したい確率分布が条件付き確率であるかそうでないかで決まります。教師なし学習は上述の枠組みでの推定です。教師ありでは $x$ であるときに $y$ である確率 $p(y|x)$ を推定します。例えば回帰分析だと、$y = f(x) + \varepsilon$ のような仮定をして、$\varepsilon$ を適当な条件付き確率分布とすることで確率モデルが得られます。$x$ の確率分布を $q(x)$ とおけば、教師ありの推定は $q(x, y) = q(x)q(y|x)$ を $q(x) p(y | x, w)$ で推定するものとみなせます。よって $q(x, y)$ を推定する教師なし学習の特殊な場合と思えます。一方で、教師なし学習は $q(x)$ が自明 (ある定数 $a$ があって、$q(x) = \delta(a -x)$) である教師あり学習と思えます。よって教師あり学習と教師なし学習は同じ枠組みで扱えます。
しかし、データの独立性の条件に少し違いがあります。$q(x, y)$ を推定する教師なし学習ではデータ $(x_i, y_i)$ の独立性を仮定しますが、教師あり学習での尤度の計算には $x$ に対する $y$ の条件付き独立性のみが必要で、$x$ の独立性は必要がありません。$x$ の独立性がないときは交差検証ができない等の違いがあるようです [渡辺3]。
目的の違い
機械学習はひとことで言うと「データからアプリケーションを作ること」だと思います。アプリケーションは多くの場合、入力 $x$ に対して出力 $y$ を得るという形式です。例えば顔認識だと、画像という入力に対して、顔の範囲とそれが誰であるかという出力が得られます。よって、アプリケーションの構成上、学習データが入力と出力のペアになっているかどうか、つまり教師ありかどうかということが気になります。
一方、統計的推定はデータを元に分析することを目的としています。例えば、コインを20回投げて表裏の出た回数を数えたとき、コインに歪みがあるのかどうかを判定する、というのは統計的推定の問題です。これは仮設検定と呼ばれるもので、基本的な考え方は次のようなものです。
まず表が出る確率と裏が出る確率を1/2であるという仮説をおきます。もし表が19回、裏が1回だとすると、それが発生する確率はものすごく低いため、仮説を棄却します。もし表が13回、裏が7回だとすると、発生する確率が低くはないので、仮説は棄却しません。ただし、確率が低いかどうかの基準は、例えば 0.05 や 0.01 など、閾値を事前に設定しておくものとします。
以上のような方法で、データから仮説が棄却できるか否かを判定します。そして、仮説が棄却できない範囲を求めることを区間推定と呼びます。この例では、入力に対して出力を得るという構造ではないことがわかると思います。データ全体を入力として、仮説が棄却されるか否かを出力とする、とも捉えられますが、それは「データからアプリケーションを作る」というよりは「データ分析のアプリケーションを作る」というのが近いように思いますので、機械学習という感じはしません。
では、統計的な分析が機械学習において必要ないかというとそうではなく、認識精度、つまりアプリケーションの質上げるためには統計的な分析が必要になります。
まとめ
数学的な枠組みの観点では機械学習と統計的推定は全く同じと言えます。強いて言えば、目的に違いがありますが、それらは排他的ではないので、無理して区別しなくて良いと思います。
参考文献
[渡辺1] 渡辺 澄夫. 代数幾何と学習理論 (知能情報科学シリーズ)
[渡辺2] 渡辺 澄夫. ベイズ統計の理論と方法
[渡辺3] 渡辺 澄夫. ベイズ統計入門 ②
