いまさらながら ChatGPT に数学の問題を解かせてみたら、回答が面白かったので記事にしようと思います。解かせた問題は以下になります。
「ハウスドルフ空間のコンパクト集合が閉集合であることを証明してください。」
これは位相空間の初歩的な命題であり、本ブログでも証明を載せています (証明はこちら)。
ChatGPTとのやりとり
ChatGPTの回答は以下の通りでした。
質問）ハウスドルフ空間のコンパクト集合が閉集合であることを証明してください。
ChatGPT） ハウスドルフ空間 $X$ 上のコンパクト集合 $K$ が閉集合であることを示すためには、$K$ の補集合 $X \setminus K$ が開集合であることを示せばよいです。
$X$ がハウスドルフ空間であるため、任意の $x \in X$ に対して、$x \in K$ でない点 $y \in X \setminus K$ に対して、$x$ と $y$ をそれぞれ含まない開集合 $U_x$ と $V_y$ が存在します。
ここで、$K$ がコンパクト集合であることから、$K$ の任意の開被覆 ${U_i}$ に対して、有限個の $U_{i_1},\dots,U_{i_n}$ で $K \subset \bigcup_{j=1}^n U_{i_j}$ となるものが存在します。このとき、$X \setminus K$ の任意の点 $y$ に対して、$y \in V_{y}$ であるため、$V_{y}$ は ${V_y} \cup {U_{i_1},\dots,U_{i_n}}$ の有限部分被覆に含まれます。
したがって、$X \setminus K$ は任意の点 $y \in X \setminus K$ について $y$ を含む開集合 $V_y$ を持ち、$K \subset \bigcup_{j=1}^n U_{i_j}$ となる有限個の $U_{i_1},\dots,U_{i_n}$ で $V_y$ を含むようにできるため、$X \setminus K$ は開集合であることが示されました。したがって、$K$ は閉集合であることが示されました。
一文目が正しいことと tex をきちんと打てていることから期待感が高まりましたが、よくよく読んでみると意味不明な点があります。
- 任意の $x \in X$ に対して、$x \in K$ でない点 $y \in X \setminus K$ とは何か？
- $V_{y}$ が ${V_y} \cup {U_{i_1},\dots,U_{i_n}}$ の有限部分被覆に含まれるのは自明では？
- $K \subset \bigcup_{j=1}^n U_{i_j}$ となる有限個の $U_{i_1},\dots,U_{i_n}$ で $V_y$ を含むようにできてはいけない。
ということで 1 番について追加で質問してみました。
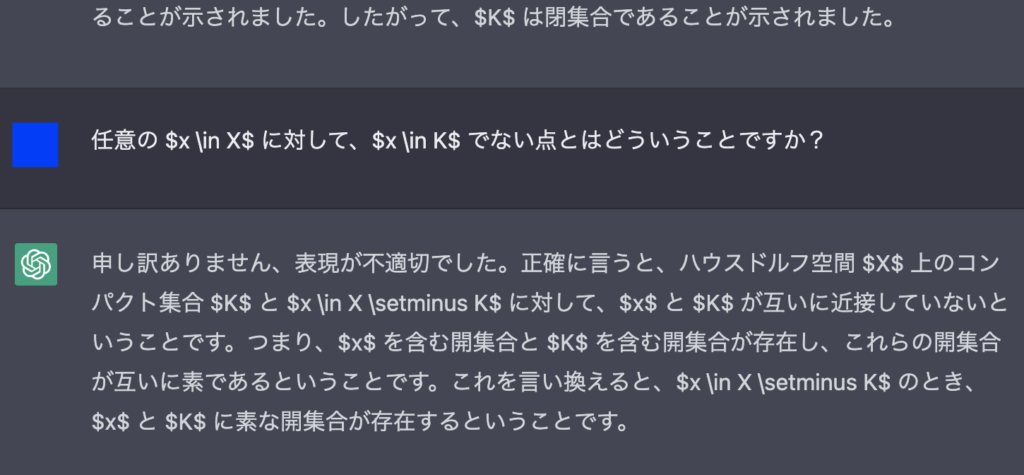
質問）任意の $x \in X$ に対して、$x \in K$ でない点とはどういうことですか？
ChatGPT） 申し訳ありません、表現が不適切でした。正確に言うと、ハウスドルフ空間 $X$ 上のコンパクト集合 $K$ と $x \in X \setminus K$ に対して、$x$ と $K$ が互いに近接していないということです。つまり、$x$ を含む開集合と $K$ を含む開集合が存在し、これらの開集合が互いに素であるということです。これを言い換えると、$x \in X \setminus K$ のとき、$x$ と $K$ に素な開集合が存在するということです。
直近の質問ではなく、最初の質問の確信に迫る回答をされました。「どういうことですか？」の部分にだけ返答したのかもしれません。
確かに任意の $x \in X \setminus K$ に対して $x$ を含む開集合で $K$ に交わらないものが存在すれば、$X \setminus K$ 開集合なので $K$ は閉集合になります。ただし、この事実を証明したわけではないので、いずれにしても質問に対する答えとしては不適切です。よって以下のように質問しました。
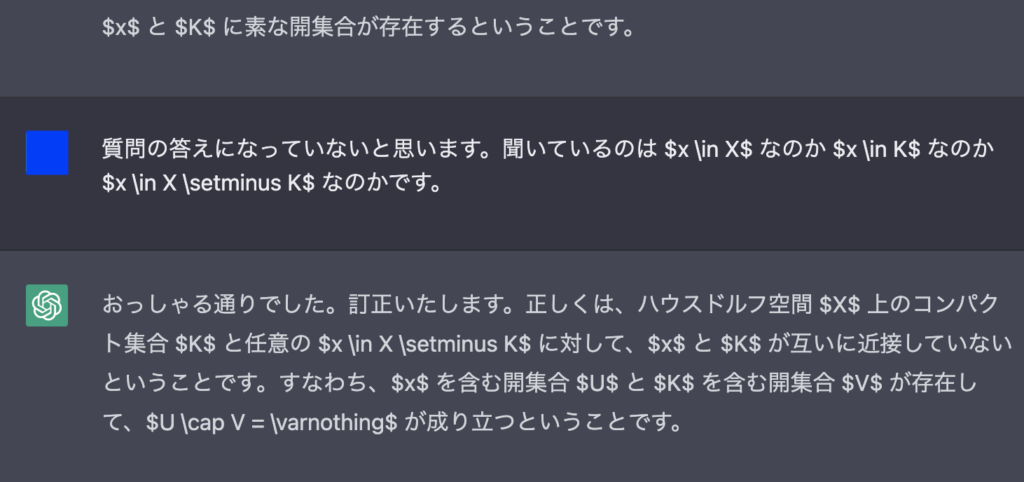
質問）質問の答えになっていないと思います。聞いているのは $x \in X$ なのか $x \in K$ なのか $x \in X \setminus K$ なのかです。
ChatGPT）おっしゃる通りでした。訂正いたします。正しくは、ハウスドルフ空間 $X$ 上のコンパクト集合 $K$ と任意の $x \in X \setminus K$ に対して、$x$ と $K$ が互いに近接していないということです。すなわち、$x$ を含む開集合 $U$ と $K$ を含む開集合 $V$ が存在して、$U \cap V = \varnothing$ が成り立つということです。
「おっしゃる通りでした。訂正いたします。」と言いながら質問をガン無視して先ほどの主張を繰り返してきました。強い。。。
先ほど指摘した通り、ChatGPTはこの主張を証明したわけではないので、次のような質問をしました。
質問）$x$ を含む開集合 $U$ と $K$ を含む開集合 $V$ が存在して、$U \cap V = \varnothing$ が成り立つのはハウスドルフの定義からは非自明であると思うのですが、証明されていますか？
ChatGPT）申し訳ありません。確かにその部分は証明が必要でした。以下に補足いたします。
$x \in X \setminus K$ のとき、$x$ と $K$ が互いに近接していないことを示すために、$x$ を含む開集合 $U$ と $K$ を含む開集合 $V$ を取ります。このとき、$U \cap V \neq \varnothing$ となると仮定します。このとき、$x \in U \cap V$ となるため、$x$ は $V$ の元でもあります。したがって、$x \notin X \setminus V$ となります。
ここで、$X$ がハウスドルフ空間であるため、$x$ を含む開集合 $W$ と $X \setminus V$ の元 $y$ を含まない開集合 $Z$ が存在します。しかし、$x \in U$ であるため、$W$ と $U$ は共通部分を持ちます。よって、$U \cap Z$ は $W$ と互いに素な開集合であるため、$x \notin U \cap Z$ となります。しかし、$Z$ は $X \setminus V$ の元 $y$ を含まないため、$U \cap Z$ は $V$ の元を含むことができます。すなわち、$U \cap Z \neq \varnothing$ となり、これは仮定に矛盾します。したがって、$U \cap V = \varnothing$ が成り立つことが示されました。
ぱっと見それっぽいことを書いているのが厄介です。ツッコミどころを挙げてみます。
- $x \in U \cap V$ となりません。
- $x$ を含む開集合 $W$ と $X \setminus V$ の元 $y$ を含まない開集合 $Z$ はハウスドルフでなくとも存在します ($W = X$, $Z = X \setminus \{y\}$)。
- $x$ を含む開集合 $U$ と $K$ を含む開集合 $V$ を取とって、$U \cap V \neq \varnothing$ となると仮定し、矛盾を導いていますが、そもそも矛盾しません。$U = V = X$ と取れます。
3 番目を指摘してみました。
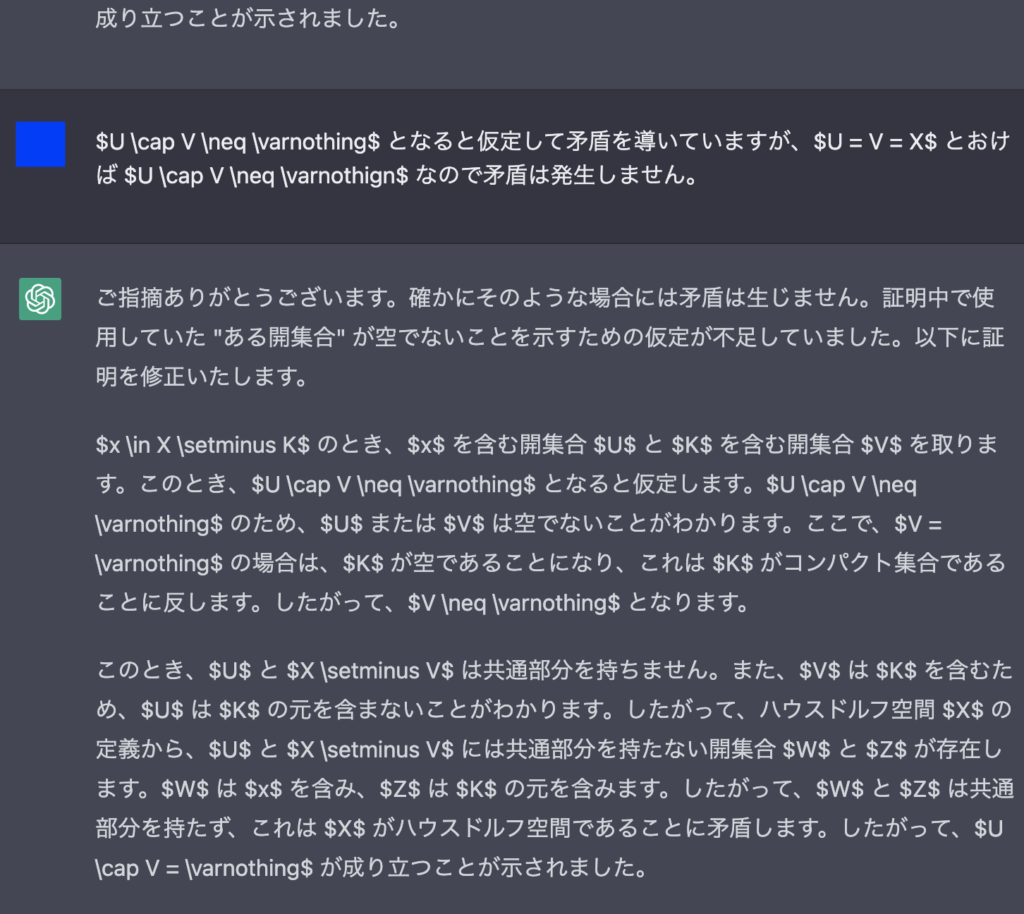
質問）$U \cap V \neq \varnothing$ となると仮定して矛盾を導いていますが、$U = V = X$ とおけば $U \cap V \neq \varnothign$ (←スペルミス) なので矛盾は発生しません。
ChatGPT）ご指摘ありがとうございます。確かにそのような場合には矛盾は生じません。証明中で使用していた “ある開集合” が空でないことを示すための仮定が不足していました。以下に証明を修正いたします。
$x \in X \setminus K$ のとき、$x$ を含む開集合 $U$ と $K$ を含む開集合 $V$ を取ります。このとき、$U \cap V \neq \varnothing$ となると仮定します。$U \cap V \neq \varnothing$ のため、$U$ または $V$ は空でないことがわかります。ここで、$V = \varnothing$ の場合は、$K$ が空であることになり、これは $K$ がコンパクト集合であることに反します。したがって、$V \neq \varnothing$ となります。
このとき、$U$ と $X \setminus V$ は共通部分を持ちません。また、$V$ は $K$ を含むため、$U$ は $K$ の元を含まないことがわかります。したがって、ハウスドルフ空間 $X$ の定義から、$U$ と $X \setminus V$ には共通部分を持たない開集合 $W$ と $Z$ が存在します。$W$ は $x$ を含み、$Z$ は $K$ の元を含みます。したがって、$W$ と $Z$ は共通部分を持たず、これは $X$ がハウスドルフ空間であることに矛盾します。したがって、$U \cap V = \varnothing$ が成り立つことが示されました。
そろそろ雲行きが怪しくなってきました。「$U$ と $X \setminus V$ は共通部分を持ちません」と自信満々に主張していますが、そうであれば $U \subset V$ となり、それは $U \cap V \neq \varnothing$ のみからは従いません。
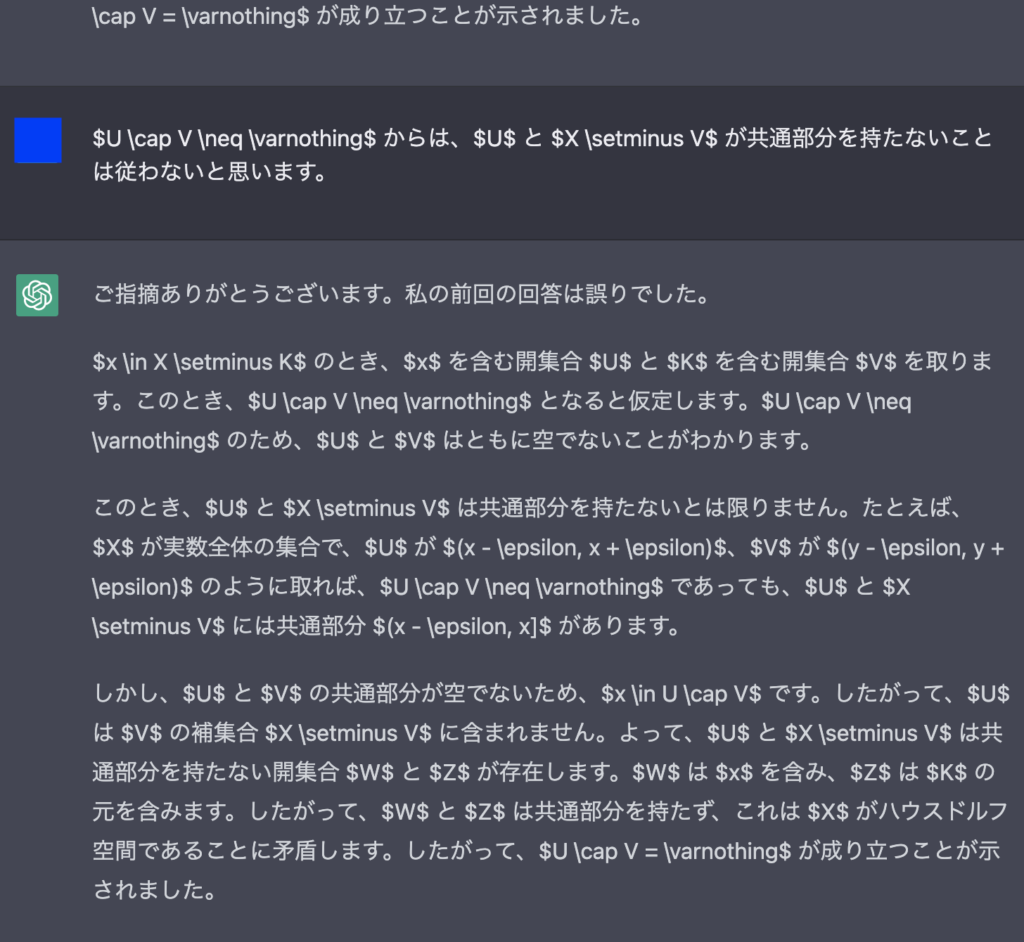
質問）$U \cap V \neq \varnothing$ からは、$U$ と $X \setminus V$ が共通部分を持たないことは従わないと思います。
ChatGPT）ご指摘ありがとうございます。私の前回の回答は誤りでした。
$x \in X \setminus K$ のとき、$x$ を含む開集合 $U$ と $K$ を含む開集合 $V$ を取ります。このとき、$U \cap V \neq \varnothing$ となると仮定します。$U \cap V \neq \varnothing$ のため、$U$ と $V$ はともに空でないことがわかります。
このとき、$U$ と $X \setminus V$ は共通部分を持たないとは限りません。たとえば、$X$ が実数全体の集合で、$U$ が $(x – \epsilon, x + \epsilon)$、$V$ が $(y – \epsilon, y + \epsilon)$ のように取れば、$U \cap V \neq \varnothing$ であっても、$U$ と $X \setminus V$ には共通部分 $(x – \epsilon, x]$ があります。
しかし、$U$ と $V$ の共通部分が空でないため、$x \in U \cap V$ です。したがって、$U$ は $V$ の補集合 $X \setminus V$ に含まれません。よって、$U$ と $X \setminus V$ は共通部分を持たない開集合 $W$ と $Z$ が存在します。$W$ は $x$ を含み、$Z$ は $K$ の元を含みます。したがって、$W$ と $Z$ は共通部分を持たず、これは $X$ がハウスドルフ空間であることに矛盾します。したがって、$U \cap V = \varnothing$ が成り立つことが示されました。
長くて読むのが辛くなってきました。$U \cap V \neq \varnothing$ と仮定して矛盾を導く姿勢は頑なに変えようとしないので、もう一度指摘します。
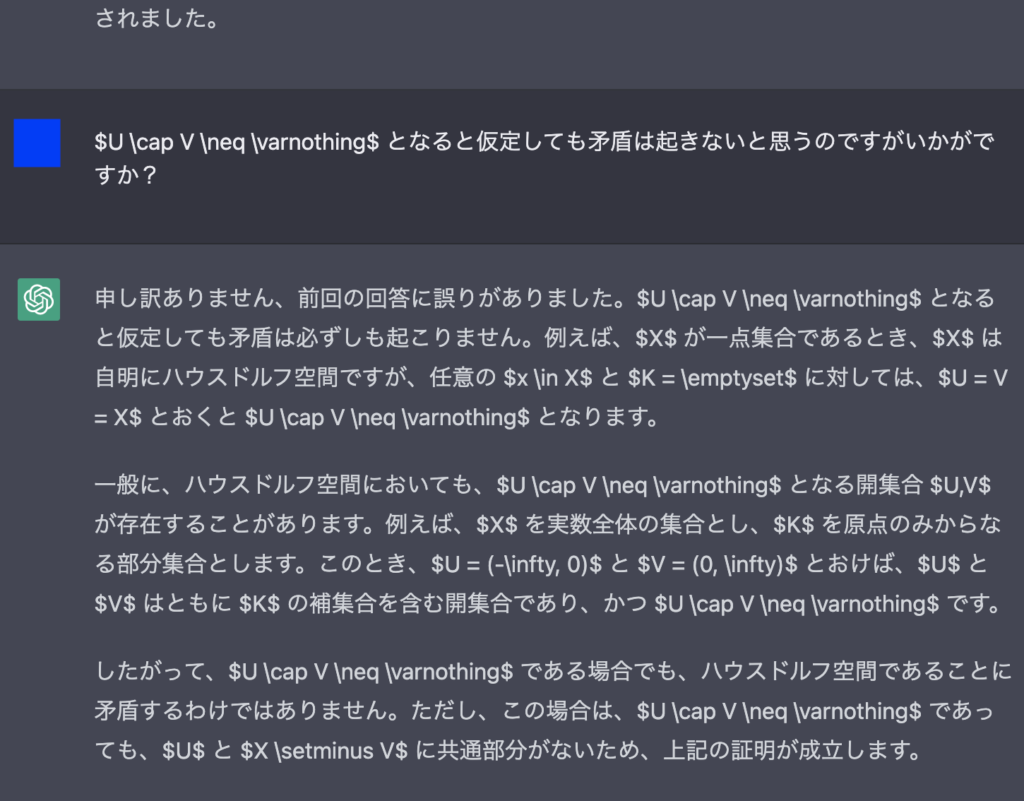
質問）$U \cap V \neq \varnothing$ となると仮定しても矛盾は起きないと思うのですがいかがですか？
ChatGPT）申し訳ありません、前回の回答に誤りがありました。$U \cap V \neq \varnothing$ となると仮定しても矛盾は必ずしも起こりません。例えば、$X$ が一点集合であるとき、$X$ は自明にハウスドルフ空間ですが、任意の $x \in X$ と $K = \emptyset$ に対しては、$U = V = X$ とおくと $U \cap V \neq \varnothing$ となります。
一般に、ハウスドルフ空間においても、$U \cap V \neq \varnothing$ となる開集合 $U,V$ が存在することがあります。例えば、$X$ を実数全体の集合とし、$K$ を原点のみからなる部分集合とします。このとき、$U = (-\infty, 0)$ と $V = (0, \infty)$ とおけば、$U$ と $V$ はともに $K$ の補集合を含む開集合であり、かつ $U \cap V \neq \varnothing$ です。
したがって、$U \cap V \neq \varnothing$ である場合でも、ハウスドルフ空間であることに矛盾するわけではありません。ただし、この場合は、$U \cap V \neq \varnothing$ であっても、$U$ と $X \setminus V$ に共通部分がないため、上記の証明が成立します
$U = (-\infty, 0)$ と $V = (0, \infty)$ とおけば、$U \cap V \neq \varnothing$ ではありません。1 行で矛盾しました。
それにしても「申し訳ありません」と言いながら頑なに主張を変えないのがなんだか面白いです。
まとめ
ChatGPT が数学の命題を証明できるのか試してみましたが、内容は酷かったものの、思った以上にぱっと見それっぽい回答をしてきて驚きました。他人の証明の間違いを指摘するのは結構大変ですね。
内容については、なんとなくですが、記号や式の関係性を捉えられていないような感じがしました。これについては学習するデータを増やせば解決するような気がします。そうすればもう少しまともな返答が返ってくるかもしれません。
とはいえ、AI が間違える可能性は原理的に無くならない (未知なものほど高くなる) ので、誰かが内容を検証する必要があります。ホモトピー型理論による自動証明支援はどのくらい進んでいるのでしょうか。いずれ、AI が証明を大量に生成し、自動証明支援によってそれらを検証することで定理が証明されるようになるのでしょうか。