「圏論的集合論 集合圏とトポス」という本で、圏論の射の像が定義されることを知りました。トポスの場合に像が構成できることも示されているのですが、図式が省略されていたり、なぜその構成で像が出来るのか少し難しい気がしたので、構成のイメージを添えて解説してみようと思います。
圏論における射の像は以下のように定義されます。
定義. 射の像
$\mathcal{C}$ を圏とし, $f : X \to Y$ を射とする. $f$ の像 (Image) を, mono射 $m: I \to Y$ で, 以下の普遍性を満たすものとする.
- 射 $e: X \to I$ で $f = m \circ e$ を満たすものが存在する。
- 同じ条件を満たす $I^{\prime}$, $e^{\prime}$, $m^{\prime}$ (対象 $I^{\prime}$ と射 $e^{\prime} : X \to I^{\prime}$, mono射 $m^{\prime} : I^{\prime} \to Y$ で $f = m^{\prime} \circ e^{\prime}$ を満たすもの) に対し, ただ一つの射 $v: I \to I^{\prime}$ が存在して、$m = m^{\prime} \circ v$ を満たす.
\begin{xy} \xymatrix { X \ar[rr]^f \ar[rd]^e \ar@[gray]@/_/[rdd]_{e^{\prime}} & & Y \\ & I \ar@{^{(}->}[ru]^m \ar@[gray]@{.>}[d]|{\exists !v} & \\ & I^{\prime} \ar@[gray]@{^{(}->}@/_/[ruu]_{m^{\prime}} & } \end{xy} $\Box$
さて、$f$ がどのような条件を満たせば、射の像を構成できるでしょうか。まず、以下のように $f$ と $f$ の pushout が存在するとします。
\begin{xy} \xymatrix { X \ar[rr]^f \ar[dd]_{f} & & Y \ar@[blue][dd]^{j_1} \\ & & \\ Y \ar@[blue][rr]_{j_2} & & Y \bigsqcup_{X} Y } \end{xy}
集合論的には、$Y \bigsqcup_{X} Y$ は $Y$ と $Y$ の非交和 $Y \bigsqcup Y$ を、同じ要素 $x \in X$ から $f$ でうつされたならば同値として、同一視したものです ($Y \bigsqcup_{X} Y$ を $f$ の cokernel pairと呼びます)。よって、集合論的には$j_1(Y)$ と $j_2(Y)$ の共通部分は $f(X)$ と一致します。これを圏論的に行うと、$j_1$ と $j_2$ の equalizer をとることになります。
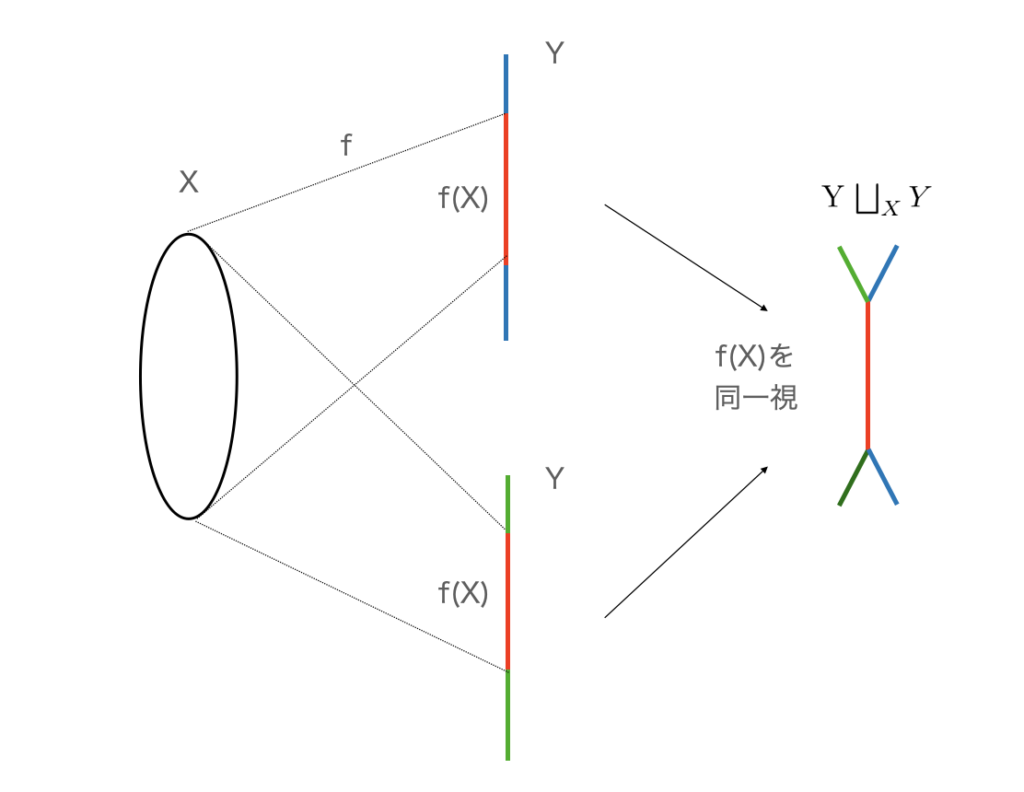
$j_1$ と $j_2$ の equalizer が存在するとしましょう。それを $m: I \to Y$ とします。equalizer なので $m$ は monic です。また、equalizer の普遍性から $e: X \to I$ で、$f = e \circ m$ となるものが唯一つ存在します。
\begin{xy} \xymatrix { X \ar[rr]^f \ar[dd]_{f} \ar@[green]@{.>}[rd]|{\exists !e} & & Y \ar@[blue][dd]^{j_1} \\ & I \ar@[green]@{_{(}->}[ld]_m \ar@[green]@{^{(}->}[ru]^m & \\ Y \ar@[blue][rr]_{j_2} & & Y \bigsqcup_{X} Y } \end{xy}
この $I, m, e$ が像の普遍性を満たすことを示したいのですが、ここで条件をもう一つ追加します。そのために、まずは定義を述べます。
定義. regular monomorphism
$m: A \to B$ を mono射とする. ある $d_1, d_2: B \to C$ が存在し, $m$ が $d_1, d_2$ の equalizer と一致するとき, $m$ を regular monomorphism という. $\Box$
$f$ が $ f = m^{\prime} \circ e^{\prime}$ と分解し、$m^{\prime}$ が mono射であるとき、$m$ が常に regular monomorphism であると仮定します。そして、先ほど構成した $I, m, e$ とは別に $I^{\prime}, m^{\prime}, e^{\prime}$ が存在するとし、$v: I \to I^{\prime}$ が一意に存在することを示します。ただし、$m^{\prime}$ はmonic とします。
仮定から $m^{\prime}$ が regular monomorphism なので、$d_1, d_2: Y \to D$ で $m^{\prime}$ が $d_1, d_2$ の equlizer と一致するものが存在します。
\begin{xy} \xymatrix { X \ar[rr]^f \ar@[green][rd]^e \ar@[gray]@/_/[rdd]_{e^{\prime}} & & Y \ar@<0.5ex>@[blue][rr]^{j_1} \ar@<-0.5ex>@[blue][rr]_{j_2} \ar@<0.5ex>@[red][rd]^{d_1} \ar@<-0.5ex>@[red][rd]_{d_2} & & Y \bigsqcup_{X} Y \\ & I \ar@{^{(}->}@[green][ru]^m & & D \\ & I^{\prime} \ar@[gray]@{^{(}->}@/_/[ruu]_{m^{\prime}} & } \end{xy}
このとき、
$$d_1 \circ f = d_1 \circ m^{\prime} \circ e^{\prime} = d_2 \circ m^{\prime} \circ e^{\prime} = d_2 \circ f$$
が成り立つので、pushout の普遍性より $j_1 \circ u = d_1, j_2 \circ u = d_2$ を満たす $u: Y \bigsqcup_{X} Y \to D$ が一意的に存在します。
\begin{xy} \xymatrix { X \ar[r]^f \ar[d]_{f} & Y \ar@[blue][d]^{j_1} \ar@[red]@/^/[rdd]^{d_1} & \\ Y \ar@[blue][r]_{j_2} \ar@[red]@/_/[rrd]_{d_2} & Y \bigsqcup_{X} Y \ar@[red]@{.>}[rd]|{\exists !u} & \\ & & D } \end{xy}
すると、
$$d_1 \circ m = u \circ j_1 \circ m = u \circ j_2 \circ m = d_2 \circ m$$
から、$d_1, d_2$ の equalizer の普遍性から、$m = m^{\prime} \circ v$ を満たす $v: I \to I^{\prime}$ が一意的に存在します。これで構成した $I$ が $f$ の像であることがわかりました。
\begin{xy} \xymatrix { X \ar[rr]^f \ar@[green][rd]^e \ar@[gray]@/_/[rdd]_{e^{\prime}} & & Y \ar@<0.5ex>@[blue][rr]^{j_1} \ar@<-0.5ex>@[blue][rr]_{j_2} \ar@<0.5ex>@[red][rd]^{d_1} \ar@<-0.5ex>@[red][rd]_{d_2} & & Y \bigsqcup_{X} Y \ar@[red]@{.>}[ld]|{\exists !u} \\ & I \ar@{^{(}->}@[green][ru]^m \ar@[red]@{.>}[d]|{\exists !v} & & D \\ & I^{\prime} \ar@[gray]@{^{(}->}@/_/[ruu]_{m^{\prime}} & } \end{xy}
以上をまとめると、以下の命題が成り立ちます。
命題. 像が存在するための十分条件
$f: X \to Y$ が次の性質を満たすとき, $f$ の像が存在する.
- $f$ の cokernel pair (つまり $f$ と $f$ の pushout) $Y \rightrightarrows Y \bigsqcup_{X} Y$ が存在する.
- $Y \rightrightarrows Y \bigsqcup_{X} Y$ の equalizer が存在する.
- $f$ が mono射 $m$ とある射 $e$ により $f = m \circ e$ と表されるとき, $m$ は常にregular monomorphismである. $\Box$
この系として、圏 $\mathcal{C}$ に常に pushout, equalizer が存在し、mono射が常に regular monomorphism であるならば、任意の射の像が存在します。トポスの場合はこれらの条件を全て満たすので、常に像が存在します。トポスのmono射が regular monomorphism であることについて軽く触れてみましょう。
トポスにおける mono 射は部分対象分類子 $\Omega$ への射に対応し、これによって mono射が equalizer で構成できます。具体的に構成すると以下のようになります。$m: X \to Y$ を mono射とし、$1$ を終対象とします。$\mathrm{True}: 1 \to \Omega$ と $\chi_{f}: Y \to \Omega$ が存在し、以下の図式の外側の四角はpullbackとなります。ここで、$!_{X}$ は終対象への唯一の射です。
\begin{xy} \xymatrix{ X \ar[r]^{!_{X}} \ar[d]_{m} & 1 \ar[d]^{\mathrm{True}} \\ Y \ar[r]_{\chi_{f}} \ar@[gray]@{.>}[ru]|{!_{Y}} & \Omega } \end{xy}
このとき、$\mathrm{True} \circ !_{Y}$ と $\chi_{f}$ の equalizer が $m$ と一致します。これは pullback の普遍性から従います。
位相空間の圏 (位相空間を対象とし、連続写像を射とする圏) $\mathbf{Top}$ の場合は、regular でない mono 射が存在します。nLabによると、$\mathbf{Top}$ の mono射は連続な単射、regular momonorphism は連続な埋め込み (値域での相対位相と同相) だそうですので、埋め込みでない単射を例に考えてみれば良さそうです。連続全単射 $f: [0, 1) \to S^{1} \ (x \mapsto e^{2\pi i x}) $ を考えましょう。もし $f$ が $d_1, d_2$ の equalizer であるとすれば、$f$ は全射なので $d_1 = d_2$ です。すると、恒等写像 $id: S^{1} \to S^{1}$ が $d_1 \circ id = d_2 \circ id$ を満たすので、$u: S^1 \to [0, 1)$ で $f \circ u = id$ になるものが存在するはずです。しかし、$f$ の逆写像は連続でないので、存在しません。
ここまで書いて思ったのですが、先ほど命題とした、射の像が存在する条件は必要条件ではありません。$f$ の圏論の意味での像は $[0, 1)$ (と $f$ )ですが、先ほどの構成方法を行うとおそらく $S^1$ が出来上がります。
参考文献
[1] 西郷 甲矢人, 能美 十三. 線型代数対話 第1巻 圏論的集合論 集合圏とトポス
[2] nLab. image, regular monomorphism
